HOY ES MIÉRCOLES 3 DE JUNIO DE 2020
HABÉIS HECHO MUY BIEN VUESTROS TRABAJOS DE PREHISTORIA.
USAD EL CORREO
ana.saco1800@gmailcom que no da problemas.
NO olvidéis vuestro rato diario de lectura.
Vamos a empezar como todos los días con
MATEMÁTICAS
REPASO
1. Fracciones
1/ 4 + 2/ 4 + 3/4 Representa esta fracción; vas a necesitar más de una unidad
3/ 7 - 1/7
1/7 x 3/6 Recuerda que era muy fácil numerador por numerador y denominador por denominador.
1/7 : 3/6 Os recuerdo
Numerador 1 x 6 Denominador 7 x 3 Total 6/21
2/8 : 1/3
2.Multiplica
2087 x 10 2087 x 100 2087 x 1.000 2087 x 105
3. Problema
La atleta Ruth Beitia en 1.998 saltó una altura de 1,89 metros.
En el año 2.014 consiguió saltar 2,01
¿Cuánto ha mejorado su marca?
NUEVO GEOMETRÍA
ÁREA DE UN TRIÁNGULO.
.
ÁREA DE UN TRIÁNGULO.
El área o superficie del triángulo que veis sería toda la parte coloreada de amarillo.
Muchas veces cuando calculáis el área del triángulo se os olvida dividir entre dos.
Siempre hay que expresar si el resultado son cm cuadrados o metros cuadrados. No vale contestar Área 14 .
TAREA
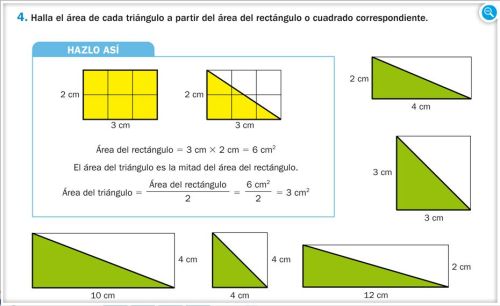Como veis la altura no tiene que estar siempre en el centro de la baseLENGUA
Hoy en lengua terminamos el trabajo sobre el CÓMIC
Creo que la tarea no es difícil y os va a gustar.
Nos centramos en las páginas 230 y 231 y hacemos los ejercicios 1,2,3 y 4.
Por supuesto, como todos los días dedicamos un rato a la lectura, para entrenar y para divertirnos.
